Aの箱とBの箱…！ぱんだBの決断の結果は・・・！ | ぱんだB漫画 | ぱんだBブログ

記事内の画像の読み込みに時間がかかるので表示されていなかったらちょっと待ってね！

たけのこの里が入っているのは箱Aなのか箱Bなのか・・・？

昨日ぱんだBが出題した問題、みなさんは回答していただいたでしょうか？！

なにそれ？という人向けにまずは一連のツイートを振り返ってみるよ！

そうそう、ぱんだBは昨日ZERO ESCAPE 刻のジレンマというゲームをクリアしたわけですが、かなり面白かったですよ！
地下シェルターに閉じ込められた９人の男女が脱出生き残りをかけて、謎の人物ゼロから仕掛けられる命がけのDecision(決断)ゲームに挑む！という内容！

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

Decisionゲームとは！二人の仲間のうち片方しか助けられないときどちらを助けるか？他チームを犠牲にすれば脱出できる早い者勝ちのボタンを押すか押さないか？という決断をあなたが自分の手で選ぶゲームです！
ちなみにぱんだBは押しちゃだめって書いてあるボタンをやりましたね。ポチッと！

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

そんな沢山の決断や謎解きを要するZERO ESCAPEからぱんだBの印象に残ったDecisionゲームを出題だ！
次のツイートでね！

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

A〜Cの３つの箱のうち一つにたけのこの里がはいっている。ぱんだBがAの箱を選ぼうとしたところ、Cの箱が突然爆発！Cの中身は空だった！
ぱんだBはまだAとBの箱どちらかを開けられる。
さあ、あなたはぱんだBにAとBどちらを開けさせる？

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

答えは明日の投票終了後に発表しますね！
なんとなく面白そうだなと思った人にはおすすめですよ！でも先に前作の善人シボウデスもやったほうがいいかも！
ZERO ESCAPE [楽天] https://t.co/rXGVG7OJ3r pic.twitter.com/8RFfXDKOUG

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

ちなみに現実のぱんだBはCの箱の前に立っていたために爆発に巻き込まれちゃいました！
ぼぉぉおおおおおんん！
あんまんまんさん！

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

ちなみにちゃんと正解はありますよ！
なぞなぞじゃないです！ぱんだBにベターな選択をさせてあげてね！
べたーん

— ぱんだB 今日は鳥栖トスTOSU戦！ (@yuzupanda_b) 2016年9月10日

というわけで、出題はこちらでした！

A〜Cの３つの箱のうち一つにたけのこの里がはいっている。ぱんだBがAの箱を選ぼうとしたところ、Cの箱が突然爆発！Cの中身は空だった！
ぱんだBはまだAとBの箱どちらかを開けられる。
さあ、あなたはぱんだBにAとBどちらを開けさせる？

ぱんだBは一体どっちの箱を開ければいいのか！

ちなみに皆さんの決断は箱Aが67%、箱Bが33％でした！

ぱんだBは皆さんの選択を信じて、箱Aを開ける！

「PANDA-B's choice is made !!!」

ぱんだBの選択が生み出したものとは…！

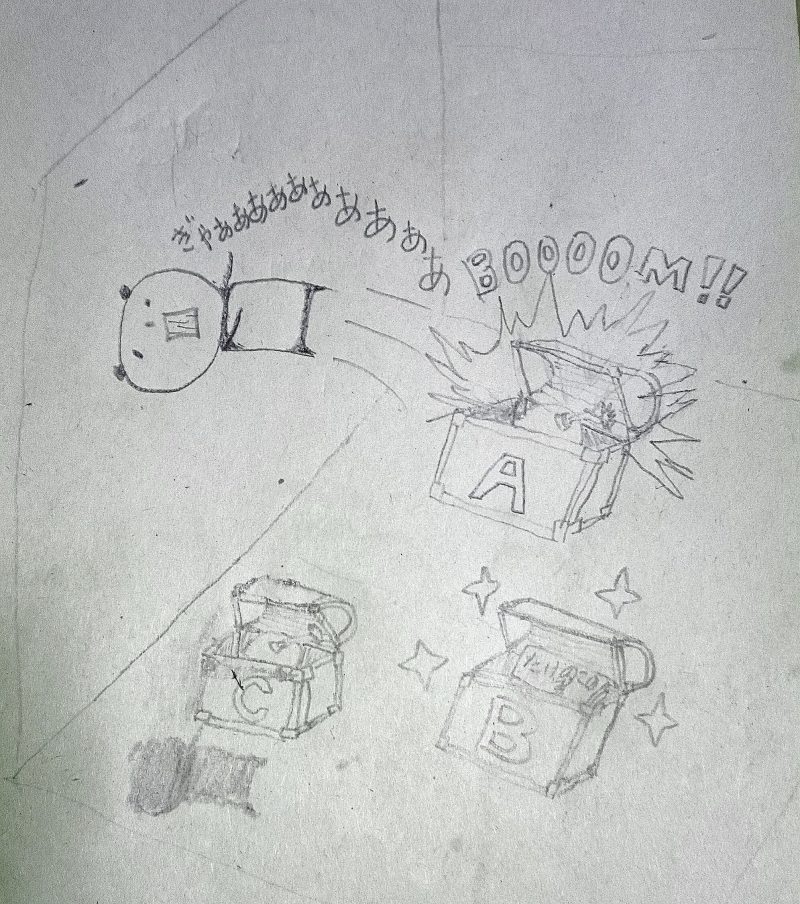
PANDA-B's choice is made !!!

※クリックで拡大

ぎやぁぁぁぁああああああああああああ！！！！！！

と、いうわけで箱AをあけたぱんだBは爆発してしまいました！
箱Aすごい！！つよい！！！勝てない！！

正解は箱Bだったんですね。
じつはこれ確率の問題なのですが、なんと箱Bにたけのこが入ってる確率はなんと箱Aの倍もあるらしいんです！

モンティ・ホール問題というそうで、有名な確率の問題なんです！
残った箱はAとBの2つだけなのになんで50%じゃなくてそんなに差がつくのか！不思議！

感覚で思い浮かべる確率と実際の確立が違うので理解しにくくはありますが、なんとかぱんだB説明してみます！

1段階目

最初にぱんだBがAの箱を選んだ時点ではA~Cの三つのどれに入っているかの確立は均等です！
これは納得だと思います！

たけのこの里が入っている確率は…

3分の1　はこA　

3分の1　はこB　

3分の1　はこC

これは納得だと思います！はこ３つでどれに入ってるかわからないので全部3分の一づつの確立で入ってる可能性がありますね！
これをはこAについて言い換えると…

2段階目

たけのこの里が入っている確率は…

3分の1　はこAに入ってる確率

3分の2　はこAに入っていない確率(はこBかはこCに入っている確率)

ここもさっきのことをはこAに入っている確率とはこAに入っていない確率で言い直しただけなのでまだ納得できると思います…！
はこAに入っている確率はもちろんさっきと変わらず3分の一。なので、箱Aに入っていない確率(箱BかCに入っている確率）は3分の２ですね！

しかしここで事件が・・・・！

箱C「俺はまだここで死ぬわけにh・・・・ぐわああああああああ！！！！」

BOOOOOOOOOM！！！！！

箱Cぃぃぃいいいいいいいいいい・・・・！

というわけで箱Cははかなく散っていったのです・・・・！

でもここでさっきの確率に異変が・・・・！

はこCが散ったところで確率が突然に変わったりはしない・・・・！
するとさっきの確率の表のはこCの文字の様子が・・・・？

たけのこの里が入っている確率は…

3分の1　はこAに入ってる確率

3分の2　はこAに入っていない確率(はこBかはこCに入っている確率)

　　　↓

たけのこの里が入っている確率は…

3分の1　はこAに入ってる確率

3分の2　はこAに入っていない確率(はこBに入っている確率)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　／BOOOOOOOOM!!!!!＼

箱Cぃぃぃいいいいいいいいいい・・・・！

なんとはこBの確率が爆上げの結果に・・・・！

つまりはこBに選択を変えるのが正解だったのです・・・・！

特に箱の中をいじったわけではないのに箱Cの爆発によって箱Bの中にある確率が増えるという不思議な感覚…！

ちょっと面白いなと思った人はZERO ESCAPE 刻のジレンマをぜひ！ぱんだBやったけど面白かったですよ！

ぱんだBはあなたのTwitterフォローをまってます！